틴매일경제

먼저 삼각형 넓이를 구하는 공식을 보겠습니다. 삼각형의 넓이는 ½×밑변×높이로 이미 초등학교 때 배웠습니다. ½을 곱하는 이유를 기억하시나요? 삼각형을 뒤집어서 붙이면 평행사변형이 만들어지는데 평행사변형의 넓이를 구하는 공식은 밑변×높이입니다. 그 넓이는 우리가 구하려는 삼각형 두 개가 합쳐져서 나온 값이기 때문에 ½을 곱하는 것입니다. 그리고 중학교 3학년이 되면 삼각비를 배우는데요. 삼각형의 넓이를 두 변과 그 끼인각을 이용해서 ½×a×b×sinC라는 공식을 학습하게 됩니다.

그럼 세 변의 길이가 각각 3, 5, 7인 삼각형의 넓이를 구해볼까요? 이 문제를 푸는 방법은 여러 가지가 있는데, 초등학교에서 배운 방법만으로는 구할 수 없습니다. 적어도 중학교 3학년 수준까지는 돼야 하는데요. 먼저 중학교 방법으로 해보겠습니다.

변의 길이가 3과 5 사이에 있는 꼭짓점을 A라고 하겠습니다. 그리고 A에서 마주 보는 변에 수선을 긋고 그 길이를 h라고 정하겠습니다. 그리고 나눠진 밑변의 길이 중 한 변을 χ라고 잡으면 다른 하나는 7-χ가 됩니다. 두 개의 직각삼각형에서 피타고라스 정리를 이용해 정리하면 h=3²-χ², h=5²-(7-χ)²이라는 식을 얻을 수 있고, h를 소거하면 χ=33/14라는 값을 얻을 수 있습니다. 이 값을 이용해서 다시 높이인 h를 구하면 h=15√3/14이 나오고, S=15√3/4이라는 넓이를 구할 수 있습니다.

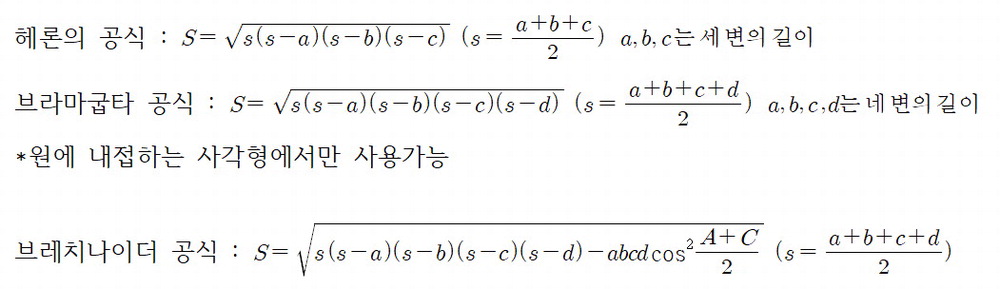
이번에는 고등학교 수학1 삼각함수 단원의 코사인법칙을 이용해서 같은 문제를 풀어보겠습니다. 코사인법칙을 이용하면 cosA=-½이 나옵니다. 이 값을 사용해서 sinA=√3/2을 구하고 같은 방법으로 넓이를 구할 수 있습니다. 중학교 방법보다는 간단하지만 미리 알고 있어야 하는 개념들이 좀 있기에 어렵게 느껴질 수도 있을 것입니다.

방금 문제처럼 세 변의 길이가 주어질 때 사용할 수 있는 더 좋은 방법이 있습니다. 그것이 바로 헤론의 공식입니다. 헤론의 공식은 삼각형의 세 변의 길이를 알고 있을 때 넓이를 구하는 간단하고 빠른 방법인데요. 헤론의 공식을 이용해서 위에서 풀었던 문제를 다시 풀어보면 s=(3+5+7)/2=15/2이므로 S=√15/2×(15/2-3)×(15/2-5)×(15/2-7)로 훨씬 빠르게 답을 구할 수 있답니다.

사각형에서도 헤론의 공식과 비슷한 식이 있습니다. 모든 사각형에서 성립하는 것은 아니고 원에 내접하는 사각형인 경우에만 성립하는데요. 바로 브라마굽타 공식입니다. 헤론의 공식에서는 세 변의 길이를 모두 더하고 반으로 나눈 것을 s라고 정했었는데, 브라마굽타 공식에서는 네 변의 길이를 모두 더한 값을 반으로 나눈 것을 s라고 약속합니다. 네 변의 길이가 각각 2, 4, 4, 6인 사각형으로 예시문제를 한번 풀어보겠습니다.

먼저 일반적인 방법으로 이 문제를 풀어볼까요. 마주 보는 두 꼭짓점을 이으면 삼각형이 두 개 만들어집니다. 원의 내접하는 사각형의 특징은 서로 마주 보는 각의 크기의 합이 180˚라는 것입니다. 위에서 나왔던 S=½×a×b×sinC 공식을 사용해서 두 삼각형의 넓이를 더해주면 S=16sinC라는 결과를 얻을 수 있는데요. sinC를 구하기 위해서는 다시 코사인법칙을 사용해야 합니다. 지면상 계산 과정을 쓰지는 않았지만 여러분은 직접 계산해서 풀어보기를 바랍니다. 우리가 구하려는 사각형의 넓이는 8√3이 됩니다. 이 문제에 브라마굽타 공식을 적용해 봅시다. 네 변의 길이를 다 더하고 반으로 나누면 8입니다. 그리고 공식에 넣어주면 바로 위에서 구한 답이 나오게 됩니다. 사실 이 문제를 푸는 쉬운 중학교 풀이가 따로 존재하는데, 그 풀이는 학생들이 직접 생각해봤으면 좋겠습니다.

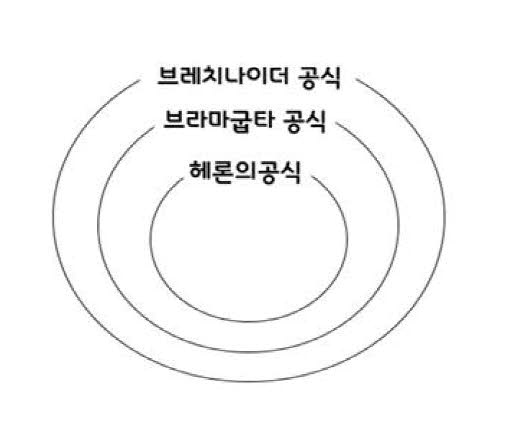
그럼 원에 내접하지 않는 일반적인 사각형의 넓이를 구하는 공식은 없을까요? 모든 변의 길이와 마주 보는 각 두 개를 알고 있을 때, 넓이를 구하는 공식이 있습니다. 브레치나이더 공식이라는 건데요. 앞 공식들과는 다르게 조금 복잡하게 생겼습니다. 브레치나이더 공식에서 뒤에 나오는 cos값은 서로 마주 보는 두 각을 더해서 구하는데 A+C가 아닌 B+D를 사용해도 같은 결과를 얻게 됩니다. 그리고 사실 이런 유형의 문제가 나온다면 삼각형 두 개로 나누어 구하는 방법이 더 나을 수도 있습니다. 뒷부분에 있는 cos값을 알지 못한다면 사용하는 의미가 없기 때문입니다. 그럼에도 브레치나이더 공식까지 소개하는 이유는 오늘 소개한 세 개의 공식이 모두 닮은 형태를 가지고 있고 서로 연관돼 있기 때문입니다.

세 공식 중 가장 일반적인 형태는 방금 소개한 브레치나이더 공식입니다. 원에 내접하는 사각형은 마주 보는 각의 크기의 합이 180˚이므로 뒷부분에 있는 cos값이 0이 되어 사라지게 됩니다. 그렇게 브라마굽타 공식이 만들어집니다.

이번에는 브라마굽타 공식에서 d=0인 경우를 생각해봅시다. 실제로 사각형에서 변의 길이가 0이 될 수는 없지만, 한 변의 길이가 점점 짧아진다고 상상을 하면 이해가 쉬울 겁니다. 그럼 그 사각형은 결국 삼각형이 되겠고 헤론의 공식이 만들어집니다.

새로운 공식을 배울 때 증명까지 해주는 것이 바람직합니다. 오늘 소개한 세 가지의 공식은 고등학교 교육과정 내에서 충분히 증명할 수 있습니다. 그러나 계산 과정이 복잡하고 어려운 내용이 조금 담겨 있어 증명을 생략하고 공식을 소개하는 정도로 이야기를 마무리 짓도록 하겠습니다. 증명을 직접 시도해보면서 여러 도전을 하는 것은 정답 유무와 관계없이 여러분의 지적 능력 향상에 도움이 될 것이니 한번 시도해보는 것을 추천합니다.