복잡함을 단순함으로 … 마법같은 수학 '행렬'
135
삶을 산다는 것은 어쩌면 선택의 연속일 것이다. 그리고 그 선택의 향방을 결정하는 중요한 요소 중 하나는 바로 '정보의 양'이다. 우리에게 제한적 정보만 제공되는 경우가 있다. 특히 투자가 그렇다. 투자를 통해 최대의 이익을 창출하는 데 있어 정보를 해석하는 능력 못지않게 '얼마나 많은 정보를 갖고 있느냐'가 중요한 과제일 것이다. 이러한 상황은 어른들만 맞닥뜨리는 것은 아니다. 학생들, 특히 시험을 치르는 수험생들에게는 제한된 정보를 해석해 전체를 파악하고 답을 도출하는 과정이 부단히 요구된다.
주어진 정보가 제한된 상황을 가정해 보자. 한 농장에서 닭과 돼지를 방목해서 기르고 있는데, 울타리와 담에 가려져 기르는 동물의 머릿수와 발의 개수만 알 수 있다. 이때 머릿수가 3개, 발의 개수가 10개라면 농장에서 키우는 닭과 돼지는 각각 몇 마리일까? 머릿수를 통해 3마리의 동물을 기른다는 것을 알 수 있고 닭의 다리는 2개, 돼지의 다리는 4개이므로 이 농장에서는 닭 한 마리와 돼지 두 마리를 키우고 있다는 것을 어렵지 않게 추측할 수 있다.
하지만 동물의 수가 이보다 많아진다면 어떨까? 예를 들어 농장에서 동물의 머릿수가 12개, 발이 40개라면 닭과 돼지를 각각 몇 마리씩 키우고 있을까? 단순하게 아래와 같은 표를 만들어 닭과 돼지의 마릿수를 직접 대입하면서 답을 생각할 수 있다.

다른 방법으로는 중학교 과정에서 배우는 '미지수가 두 개인 연립일차방정식'을 활용할 수도 있다. 닭의 마릿수를 x, 돼지의 마릿수를 y라고 했을 때 우리는 x+y=12 …①이라는 방정식을 세울 수 있고, 동물들의 다리 개수를 통해 2x+4y=40…②라는 식도 세울 수 있다. ①번식을 x=12-y로 변형해 ②번식에 대입하면 2(12-y)+4y=40이라는 식을 얻을 수 있고, 이를 통해 y=8, 즉 돼지가 8마리이며, 닭은 4마리라는 것을 알 수 있다.
만일 상황이 더욱 복잡해진다면 어떨까? 위 경우에는 닭과 돼지, 두 종류 동물의 마릿수를 미지수로 하는 방정식을 통해 답을 얻었지만, 미지수가 훨씬 많은 경우라면 이와 같은 방법으로는 쉽게 답을 찾기 어려울 것이다.
특별한 형태의 연립방정식을 예시로 들어본다.
x - 2y - z=1 …①
y + 2z = 5 …②
z = 3 …③
연립일차방정식에서 ③번식의 z값을 ②번식에 대입하면 y값을 구할 수 있고, 여기서 얻은 두 변수의 값을 ①번식에 대입하면 x의 값을 구할 수 있다. 이러한 과정과 각 식에서 생략된 변수를 다시 연립방정식으로 표현하고, 각 식의 계수와 우변의 상수항만을 사용해 순서에 따라 다른 형태로 써보면 아래와 같다.

오른쪽 표현법에서 가장 오른쪽 열의 숫자인 2, -1, 3은 처음 제시된 연립방정식의 해인 x, y, z의 값과 일치한다는 것을 알 수 있다. 동시에 같은 정보를 보다 간결하게 나타낼 수 있다는 것도 확인할 수 있다. 오른쪽 표현처럼 연립일차방정식의 상수들을 나열한 방식을 '첨가행렬'이라고 하고, 각 상수를 '성분'이라고 한다. 연립일차방정식을 첨가행렬로 표현하고, 각 행을 연산을 통해 아래와 같이 만들어도 연립일차방정식의 해를 구할 수 있다.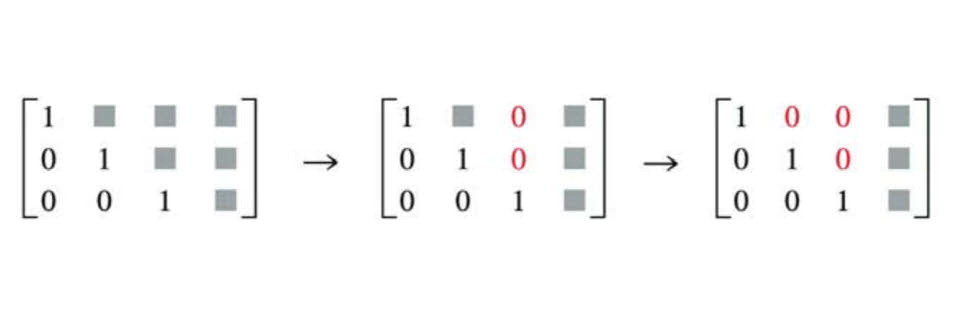
위 단계를 거쳐 정리된 형태의 행렬을 '기약행사다리꼴'이라고 하며, 이를 이용해 연립방정식의 해를 구하는 방법을 '가우스-요르단(조던) 소거법'이라고 한다. 가우스 소거법이 소개된 이후 독일의 측지학자인 요르단(Wilhelm Jordan)이 이를 개선하고 역대입법을 체계화시켜 연립일차방정식을 대각선 형태로 만드는 알고리즘을 개발해 이와 같은 이름을 붙인 것이다.
지금까지 내용을 통해 우리는 연립방정식 계수만을 통해 그것의 해를 구할 수 있다는 것을 알았다. 그렇다면 모든 연립방정식은 특정한 해가 존재할까? 그렇지 않다. 해가 존재하지 않는 경우도 있으며, 무수히 많은 해가 존재하는 경우도 있다. 그럼 '연립일차방정식의 계수만으로 해의 존재를 알 수 있는 방법이 없을까'라고 생각해 볼 수 있다. 일본 에도시대의 수학자인 세키 고와(關孝和)와 독일의 수학자인 라이프니츠(Gottfried Wilhelm Leibniz)는 이러한 착상을 바탕으로 계수를 통해 주어진 연립일차방정식이 유일한 해를 갖는지를 알아내는, 현대적 의미의 '행렬식'에 대한 연구를 진행했다.
역사적으로 행렬식에 대한 연구가 선행됐고, 이후 그것의 모체가 되는 '행렬'에 대한 연구가 진행됐다. 행렬이란 용어는 영국의 수학자인 실베스터(James Joseph Sylvester)가 처음 사용한 것으로 m행과 n열로 이뤄진 수의 직사각형 배열로 도입됐다. 이후 영국의 수학자인 케일리(Arthur Cayley)는 연립일차방정식을 행렬로 표현하고, 동시에 일차변환의 표현으로 행렬의 의미를 파악했다.
케일리는 두 일차변환의 합성변환에 대해 연구하면서 '행렬의 곱셈'을 정의했다. 통상적으로 곱셈은 순서를 바꿔도 결과는 같다. 이것을 '곱셈의 교환법칙'이라고 한다. 하지만 행렬의 곱셈은 다르다. 즉, 곱셈의 교환법칙이 성립하지 않는 비가환성을 행렬을 통해 인식하게 된 것이다. 이는 기존의 대수학을 넘어서는 아이디어를 얻게 되는 계기가 됐다.
교육과정 개편을 통해 고등학생들은 다시 행렬에 대해 배우게 됐다. 2009 개정 교육과정 이후 일반과목에서 삭제됐던 행렬이 왜 다시 도입된 것일까? 인공지능(AI), 정보통신기술(ICT)이라는 단어로 대변되는 오늘날 과학기술 사회에서는 공학 및 자연과학 분야에서 수학적 모델링을 통해 문제 해결의 중요성이 부각되고 있다. 이때 사용되는 수학적 모델은 주로 복잡한 방정식의 형태를 띠고 있다. 하지만 그것의 구체적인 해를 찾기란 쉽지 않다. 그래서 구체적인 해보다는 컴퓨터 계산을 이용한 근사해를 구하는 문제로 귀결된다. 행렬은 이러한 대규모 계산의 용이성을 위해 사용되는 동시에 통계, 물리, 경제, 공학 등 수학 이외의 분야에서 여러 값이 포함된 자료를 효율적으로 다루는 도구로 활용되고 있다.
2022 개정 교육과정 과목 중 '경제수학'에 '행렬과 경제'가 신설됐다는 점만 보더라도 행렬의 높은 활용도를 짐작해 볼 수 있다. 행렬은 복잡함을 간결하게 만들어 준다. 간결함은 어떤 문제의 본질을 파악하는 데 유용하다. 스위스의 수학자인 오일러(Leonhard Euler)가 쾨니히스베르크 다리 문제를 풀기 위해 다리는 선으로, 섬과 육지는 점으로 단순화시켜 접근했듯이 수학, 특히 행렬은 문제를 대할 때 우리의 판단과 선택을 용이하도록 도와주고 우리의 결정을 합리적으로 이끌어 주는 요체가 된다.
해설 및 정답
정답: ⑤








